Tổng hợp Áp dụng sơ đồ Hoocne (Horner) để chia đa thức một cách dễ hiểu nhất là vấn đề trong nội dung bây giờ của tôi Tablenow.vn. Theo dõi nội dung để hiểu thêm nhé.
1. Giới thiệu về sơ đồ Hoocne
Phân tích đa thức thành các nhân tử là kiến thức cơ bản trong các bài học về nhân chia đơn thức, đa thức, đặc biệt trong các biểu thức phân số có biến hoặc chia đa thức trong chương trình toán lớp 8 và các lớp tiếp theo.
Có nhiều phương pháp để phân tích đa thức thành nhân tử. Tuy nhiên, một số bài toán đa thức có thể gây khó khăn cho học sinh trong việc thực hiện phân tích này.
Sơ đồ Horner là một thuật toán được thể hiện dưới dạng sơ đồ, giúp nhanh chóng tìm ra thương và dư khi chia một đa thức f(x) cho đa thức x−c, với c là một số thực bất kỳ.
2. Các phương pháp áp dụng
2.1 Sử dụng kiến thức toán học
Sơ đồ Horner (Hoocne/ Hoắc – le/ Hắc – le) được dùng để tính toán thương và dư khi chia đa thức f(x) cho đa thức x – α. Quy trình thực hiện như sau:
Giả sử có đa thức
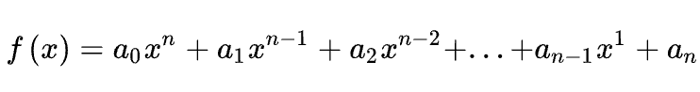
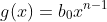

Quy trình thực hiện theo các bước như sau:
Bước 1 Bước 2
Bước 2 Bước 3
Bước 3
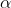
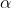
Quy tắc nhớ: NHÂN NGANG, CỘNG CHÉO.
Bước 4: Tiếp tục như vậy cho đến khi xử lý hết các hệ số, và kết quả cuối cùng sẽ là
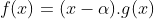
tốt

* Lưu ý:
+ Bậc của đa thức g(x) luôn thấp hơn bậc của đa thức f(x) một đơn vị vì đa thức chia x – a có bậc bằng 1.
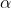
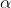
2.2 Sử dụng máy tính CASIO
Phương pháp này rất tiện lợi khi đa thức có bậc cao, hệ số lớn hoặc có các số phức tạp.
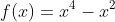
Bước 1: Tạo bảng như mô tả bên dưới (nếu bạn nhớ tốt, có thể thực hiện trực tiếp mà không cần lập bảng)
.png)
Bước 2. Nhập hệ số đầu tiên vào dòng dưới => sau đó nhấn phím =

Bước 3. Nhấn phím AC => sau đó nhập cAns+X, c là -1
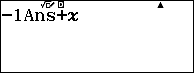
Bước 4. Nhấn CALC rồi nhập hệ số thứ hai vào dòng trên, ở đây là 0, sau đó nhấn phím = để nhận hệ số thứ hai của dòng dưới.
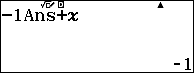
Bước 5. Lặp lại Bước 4 cho các hệ số còn lại.
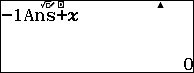
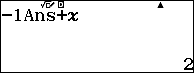
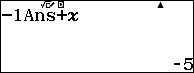
3. Một số bài tập trắc nghiệm để thực hành
Bài 1: Kết quả của phép chia ( 7x^3 – 7x + 42 ) chia cho ( x^2 – 2x + 3 ) là gì?
A. – 7x + 14 B. 7x + 14
C. 7x – 14 D. – 7x – 14
Giải đáp:
Chúng ta thực hiện phép chia
.png)
Lựa chọn đáp án B.
Bài 2: Khi chia x^3 + x^2 – 4x + 7 cho x^2 – 2x + 5, đa thức dư là gì?
A. 3x – 7. B. – 3x – 8.
C. – 15x + 7. D. – 3x – 7.
Giải đáp
Chúng ta có phép chia
.png)
Dựa trên kết quả phép chia, đa thức dư thu được là – 3x – 8.
Chọn đáp án B.
Bài 3: Xác định hệ số a sao cho đa thức 4x² – 6x + a chia hết cho x – 3?
A. a = – 18. B. a = 8.
C. a = 18. D. a = – 8.
Giải thích:
Ta thực hiện phép chia.
.png)
Kết quả phép chia là số dư (a + 18).
Để đa thức 4x² – 6x + a chia hết cho x – 3 ⇔ a + 18 = 0 ⇔ a = – 18.
Chọn đáp án A.
Bài 4: Thực hiện phép chia: (4x⁴ + x + 2x³ – 3x²) : (x² + 1) và xác định số dư.
A. – x + 7
B. 4x² + 2x – 7
C. 4x² – 2x + 7
D. x – 7
Giải thích:
Ta có: 4x⁴ + x + 2x³ – 3x² = 4x⁴ + 2x³ – 3x² + x
.png)
Do đó: (4x⁴ + x + 2x³ – 3x²) = (4x² + 2x – 7) . (x² + 1) – x + 7
Chọn đáp án A
Bài 5: Thực hiện phép chia (3x³ + 2x + 1) : (x + 2) và tìm đa thức dư.
A. 10 B. -9
C. – 15 D. – 27
Giải thích:
Ta có:
.png)
Số dư của phép chia là –27.
Chọn đáp án D
Bài 6: Thực hiện phép chia (-4x⁴ + 5x² + x) : (x² + x) và xác định kết quả.
A. – 4x⁴ + 5x² + x = (x² + x) . (-4x² – 4x + 9) – 6x
B. – 4x⁴ + 5x² + x = (x² + x) . (4x² + 4x + 9) + 12x
C. – 4x⁴ + 5x² + x = (x² + x) . (-4x² + 4x + 9) – 8x
D. – 4x⁴ + 5x² + x = (x² + x) . (4x² – 4x + 9) + 10x
Giải thích:
Ta có:
.png)
Kết quả là –4x⁴ + 5x² + x = (x² + x) . (-4x² + 4x + 9) – 8x
Chọn đáp án C
Bài 7: Xét phép chia: (x³ + 9x² + 27x + 27) : (x + 3). Tìm khẳng định sai.
A. Phép chia này là phép chia hết
B. Thương của phép chia là: (x + 3)²
C. Thương của phép chia là: x² + 6x + 9
D. Số dư của phép chia là: x – 3
Giải thích:
Áp dụng hằng đẳng thức đáng nhớ:
(a + b)³ = a³ + 3a²b + 3ab² + b³, ta có:
(x³ + 9x² + 27x + 27) : (x + 3) = (x + 3)³ : (x + 3) = (x + 3)² = x² + 6x + 9
Do đó, phép chia là phép chia hết với thương là: (x + 3)² = x² + 6x + 9.
Chọn đáp án D
Bài 8: Thực hiện phép chia: (x²y + 4xy + 3y) : (x + 1) và xác định thương.
A. xy + 3 B. x + 3y
C. x + y + 3 D. y . (x + 3)
Giải thích:
Ta có: x²y + 4xy + 3y = y . (x² + 4x + 3)
= y.[(x² + x) + (3x + 3)]
= y.[x.(x + 1) + 3(x + 1)]
= y.(x + 3).(x + 1)
Do đó: (x²y + 4xy + 3y) : (x + 1) = y.(x + 3).(x + 1) : (x + 1) = y.(x + 3).
Chọn đáp án D
Bài 9: Tìm giá trị a sao cho phép chia (x³ – 4x + a) : (x – 2) là phép chia hết:
A. a = 0 B. a = 4
C. a = -8 D. a = 8
Giải thích:
Ta có:
.png)
Phép chia sẽ là phép chia hết khi phần dư bằng 0. Do đó, a = 0.
Chọn đáp án A
Bài 10: Thực hiện phép chia: (9x³y² + 10x⁴y⁵ – 8x²y²) : x²y²
A. 9x + 10x²y² B. 9 + 10x²y² – 8
C. 9x + 10x²y³ – 8 D. Đáp án khác
Giải thích:
Ta có: (9x³y² + 10x⁴y⁵ – 8x²y²) : x²y²
= 9x³y² : x²y² + 10x⁴y⁵ : x²y² – 8x²y² : x²y²
= 9x + 10x²y³ – 8
Chọn đáp án C